Bestandsoptimierung bei Ersatzteilen mithilfe guter Prognosen

Die unendliche Lebensdauer einer Maschine wäre für jedes Produzenten natürlich ein Traum. Die Realität sieht anders aus. Immer mal wieder fällt etwas aus und der Produzent benötigt Ersatzteile.
Wäre es nicht toll, wenn Sie genau dieses Ersatzteil genau dann, wenn es benötigt wird, auf Lager haben?
Ein Sicherheitsbestand von entsprechenden Ersatzteilen dient dazu, diesem Wunsch entgegenzukommen. Mit einer datenbasierten, methodischen Herangehensweise lassen sich die eigenen Ersatzteilbestände optimieren. Welche entscheidende Rolle gute Prognosen hierbei spielen, erläutern wir an einem Beispiel.
Bestandsoptimierung bedarf Bedarfsplanung
Falsche Bestände verursachen Kosten
Erstes Szenario:
Eine Maschine, die aufgrund des Ausfalls eines Maschinenteils nicht funktionsfähig ist, kostet. Die Produktion kann nicht im gewünschten Umfang stattfinden und steht im schlimmsten Fall sogar komplett still:
Es kommt zu Umsatzausfällen
Die Bediener der Maschine können nicht ihrer geplanten Arbeit nachgehen.
Sie lesen einen Beitrag der Autoren von prognostica
Sie lesen einen Beitrag der
Autoren von prognostica
Zweites Szenario:
Die Maschine wird am Ende ihrer Lebenszeit in den Ruhestand verabschiedet. Möglicherweise ist die Technik überholt, die Teile, die sie produziert, werden nicht mehr benötigt oder sie ist schlichtweg defekt. Weder sie noch eine andere Maschine im Unternehmen benötigen noch Unmengen an Ersatzteilen, die die Instandhaltung an Lager gelegt hat. Es hilft nur noch die Abschreibung. Es entstehen unnötige Kosten durch den Erwerb und die Lagerung der nicht benötigten Teile.
Der Idealfall
Optimalerweise würde die Instandhaltung beim Ausfall eines Maschinenteils kurz den Lagerbestand prüfen und feststellen:
das benötigte Ersatzteil steht zur Verfügung
Es wird eingebaut, und die Maschine und mit ihr die Produktion laufen nach einer nur kurzen Unterbrechung weiter. Der Lagerbestand ist zudem nicht absurd hoch, sondern entspricht möglichst genau dem Bedarf an Ersatzteilen. Falls nötig, kann das Ersatzteil in der gewünschten Menge rechtzeitig nachbestellt werden.
Wir nehmen wir ein solches Ersatzteil genauer in Betracht und versuchen uns den Fragen zu nähern:
- können wir den Bedarf an diesem Ersatzteil in der relevanten Menge zu den relevanten Zeitpunkten ermitteln?
- wie können wir daraus einen praxistauglichen Sicherheitsbestand berechnen, der beinhaltet, wie viele dieser Ersatzteile man sicherheitshalber auf Lager legen sollte?
- wie lassen sich auch zufällige (und ungewöhnliche) Bedarfsschwankungen in der Zukunft zumindest meistens bedienen?
- in welchem Umfang können wir auf diese Weise Produktionsstopps, Umsatzausfälle, Abschreibungen oder unnötig hohe Lagerkosten vermeiden?
Wir machen zunächst eine Bestandsaufnahme. Dazu wollen wir uns in diesem Use Case dem Problem datengetrieben nähern. Insofern interessieren wir uns für Datenbestände, bereits verwendete und potenziell verwendbare Ansätze zur Datenverarbeitung und -analyse.
Vor der Bestandsoptimierung für Transparenz sorgen
Um ein Gespür für die Gegebenheiten des vorliegenden Falles zu bekommen, empfiehlt sich frühzeitig eine Visualisierung. Als ersten Schritt in diese Richtung schauen wir uns einmal die historischen realisierten Abgänge bzw. Verkäufe des Produktes kompakt in einer Grafik an. Und zwar auf Tagesebene:
Zeitreihe der historischen Verkäufe eines Ersatzteils auf Tagesebene
Die Historie weist ein sporadisches Muster auf, d.h. es gibt viele Tage, an denen wir keine Abgänge des Produkts beobachten. Eine solcher Zeitreihen ist recht typisch für Ersatzteile. Gäbe es Auffälligkeiten in den Daten, wie z.B. lange Zeiträume ohne Nachfrage, könnte man diese leicht erkennen und entsprechende Schlussfolgerungen ziehen.
Als Erweiterung der Visualisierung könnten Sie z.B. Zu- und Abflüsse des Ersatzteils oder Lagerbestände plotten. Zahlen, die im ERP-System alleine oft harmlos aussehen, aber in Form und Farbe schnell potenzielle Verbesserungsmöglichkeiten offenlegen.
Wiederbeschaffungszeiten und Co.: Welche Größen existieren im System?
Formeln zur Berechnung von Sicherheitsbeständen nehmen die erfassten Bedarfshistorien — hier die täglichen Abgänge der vergangenen vier Monate — sowie potenziell weitere Parameter in Betracht. Daraus ermitteln wir einen empfohlenen Wert. Dabei gibt es eine Reihe von heuristischen Methoden bis hin zu sehr ausgefeilten Methoden mit unterschiedlichsten Parametern.
Wir schauen für unseren Fall einmal genauer hin:
- welche Größen gibt es im System?
- findet sich die Wiederbeschaffungszeit eines Teils, ihre Varianz bzw. Standardabweichung, in diesem oder einem anderen System?
- können sie anhand von historischen Bestell- und Lieferdaten ermittelt werden?
- wenn ja, wie gut sind sie gepflegt?
- ist es eine Option, diese ins Vorgehen zur Bestandsoptimierung zu integrieren?
In unserem Fall ist die Wiederbeschaffungszeit des Ersatzteils bekannt. Wir können sie daher als deterministische Größe in die Berechnung einbeziehen.
Bedarfsplanung in der Realität
Je besser man die künftigen Bedarfe eines Ersatzteils kennt, desto gezielter kann man sich genau die richtigen Mengen zum richtigen Zeitpunkt auf Lager legen.
Wie werden diese voraussichtlich benötigten Mengen aktuell ermittelt?
Nicht selten verwenden Unternehmen an dieser Stelle Standardeinstellungen im ERP-System. Oder sie setzen benötigte Prognoseverfahren und zugehörige Parameter aufgrund der Erfahrung einzelner Planer fest. Auch wird einem zu planenden Ersatzteil oder Material oft das gleiche Verfahren übergestülpt wie den meisten anderen, ohne diesen Fall noch einmal separat zu hinterfragen. Oder aber Planer tragen die zukünftigen voraussichtlichen Abgänge im Wesentlichen manuell ein.
Dabei stellen wir oft fest, dass sich Planer bei wichtigen und voluminösen Artikeln besonders viel Mühe geben, während andere Artikel aufgrund von Zeitmangel keine Beachtung finden.
Nicht selten ist es jedoch so, dass häufig verkaufte Artikel eine relativ stabile Datenhistorie mitbringen, die durch quantitative Verfahren gut vorhersagbar ist. Der Planer kann durch eine manuelle Planung hier oft gar nicht ein Mehr an Planungsgüte erzielen. Sinnvoller wäre es, die Zeit in die Prognose neuer Artikel, Sonderfälle oder solche mit besonders volatiler Datenhistorien zu stecken.
Durch Prognosen die voraussichtlichen Bedarfe des Ersatzteils ermitteln
Wir legen vor diesem Hintergrund daher Augenmerk auf die Fragen:
- wie gehen wir mit der besonderen Beschaffenheit der Datenhistorie um?
Vor allem im Hinblick auf die sporadische Natur unserer Ersatzteil-Zeitreihe? - welches Maß wenden wir an, um die Güte der Prognosen zu beurteilen?
- wird dies der sporadischen Beschaffenheit der Bedarfshistorie gerecht?
Prognoseverfahren profitieren enorm von der Vollständigkeit und Korrektheit der Daten. Das gilt insbesondere, sofern die Rahmenbedingungen invariant sind, von einer ausreichenden Länge der Datenhistorie. Im Normalfall werden die letzten zeitlich zurückliegenden Ersatzteil-Bedarfe für die Prognosen verwendet.
Bei Prognosen auf Monatsbasis sind das beispielsweise idealerweise die letzten drei bis fünf oder sogar mehr Jahre an monatlichen Werten. Bei sporadischen Zeitreihen sollten ausreichend viele nichtnegative Bedarfe beobachtet worden sein.
Manchmal kann es sinnvoll sein, neuere Ersatzteilhistorien mit älteren zu matchen, die sich sehr ähnlich sind oder sachlogisch zusammengehören. Je länger eine gut gepflegte und aussagekräftige Datenhistorie ist, desto besser.
Auf Tagesbasis kommen wir mit den in unserem Fall vorhandenen etwa vier Monaten an lückenlosen täglichen Daten gut aus. Darauf basierend ermitteln wir Sicherheitsbestände .
Bestandsplanung für Ersatzteile: ein naiver Ansatz
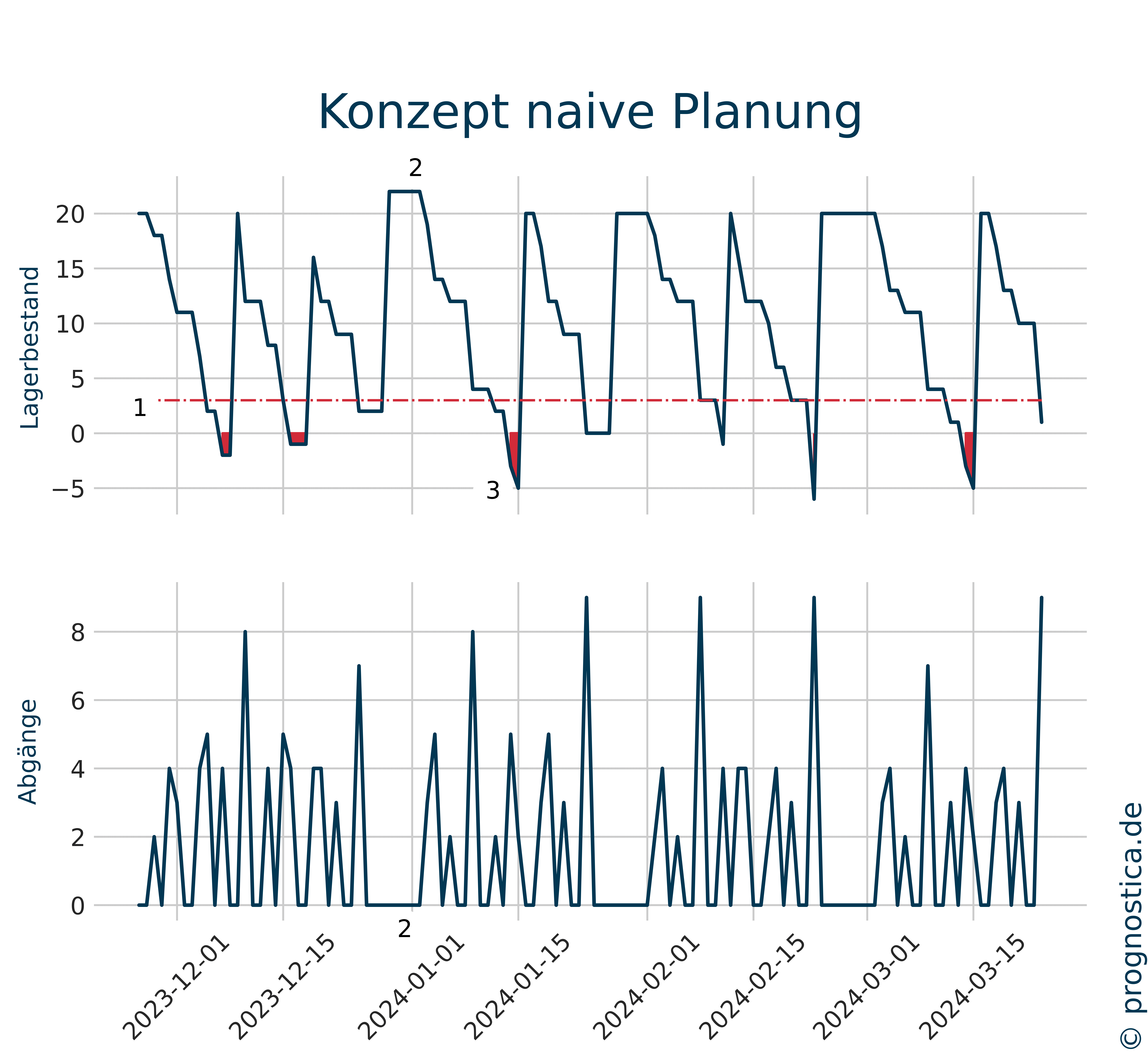
Für unser Beispiel stellen wir zunächst einen naiven Ansatz vor, den man in ähnlicher Weise in der Praxis oft beobachten kann. Bei diesem Ansatz starten wir mit einem Lagerbestand von 20 Ersatzteilen. Die Wiederbeschaffungszeit des Ersatzteils beträgt im Modell vier Tage. Jeden Tag werden dem Lager eine gewisse Zahl Ersatzteile größer gleich Null entnommen, entsprechend dem jeweiligen Bedarf. Sobald der Lagerbestand einen kritischen Wert von drei Teilen (untenstehende Grafik: rote gestrichelte Linie (1)) erreicht hat, werden 20 nachbestellt. Aufgrund der Wiederbeschaffungszeit von vier Tagen wird diese Maßnahme erst verzögert wirksam.
Bei der Planung sind vor allem zwei Aspekte miteinander in Einklang zu bringen:
- Sind die Sicherheitsbestände pauschal zu hoch angesetzt, wird vor allem in Zeiten geringer Abgänge — siehe Phase 2 in der Grafik — unnötig viel auf Lager gehalten.
- Setzt man die Sicherheitsbestände zu niedrig an, kann dies hingegen dazu führen, dass Fehlteile auftreten — siehe Phase 3 in der Grafik.
Entwicklung der Bestände bei Anwendung einer naiven Bestandsplanung
Betrachtet man in der Grafik beispielhaft die letzten 30 Tage, fällt auf, dass alternierend sowohl unnötig hohe Lagermengen als auch Lieferengpässe auftreten. Der naive Ansatz zur Bestandsplanung erzeugt unnötige Bestandskosten. Potenzielle Kundenabwanderung bedroht das Ersatzteilgeschäft.
Entwicklung der Bestände über einen Zeitraum von 30 Tagen bei Anwendung einer naiven Bestandsplanung
Wir sehen im Folgenden, wie man diesen Prozess mit fundierten Prognoseverfahren verbessern kann.
Mit guten Prognosen zu guten Sicherheitsbeständen und zur Bestandsoptimierung
Aus unserer vollständigen, gut gepflegten Historie der Ersatzteil-Bedarfe über die Zeit leiten wir Prognosen ab. Bei der Vorhersage sporadischer Bedarfe kommen viele übliche Vorhersageverfahren nicht in Frage. Das liegt insbesondere daran, dass sie beispielsweise nicht mit Zeiträumen ohne Bedarfe (Nullwerte) umgehen können. Damit verbleibt eine Reihe von Prognoseverfahren für sporadische Bedarfe, die sich hierfür eignen.
Da fast jeder Ersatzteil-Fall etwas anders ist als der andere, betrachten wir unser Planungsobjekt einzeln, um herauszufinden, welche Verfahren mit welchen Einstellungen in diesem Fall die besten Ergebnisse erzielen. Rückblickende Analysen sind besonders nützlich:
- Wie gut hätte ein Prognosemodell funktioniert?
- Welche Prognosegüte hätte das eine oder andere Modell erzielen können?
Eine Aussage über die konkrete Güte oder das Optimierungspotenzial des einen oder anderen Verfahrens lässt sich dabei nur schwer bis gar nicht von vornherein treffen. Es hilft nur, die grundsätzlich geeigneten Verfahren auszuprobieren. Da wir eine sporadische Zeitreihe vorliegen haben, richtet sich unser Blick hierbei in erster Linie auf die Prognosegüte- bzw. Fehlermaße SPEC und PIS, die im Kontext der Bestandsentwicklung besonders gut die mit einer Lagerhaltung verbundenen Kosten quantifizieren. In unserem Fall ergibt die Analyse, dass das Median-Pattern-Modell — ein statistisches Verfahren, das gut auf sporadischen Zeitreihen funktioniert — mit einer Pattern Length von 30 sehr gute Prognosen ergibt.
Ergebnis der Modell-Auswahl für Prognosen
In der folgenden Grafik sehen wir, wie wir für unsere sporadische Ersatzteilbedarfs-Zeitreihe Prognosen für die nächsten Monate abgeleitet haben. Schließlich lässt die Zeitreihe der Bestellungen ein klares, sich wiederholendes Muster erkennen. Das Median-Pattern-Verfahren konnte sich dies zunutze machen:
Entwicklung der Bestände über einen Zeitraum von 30 Tagen bei Anwendung eines passenden datenbasierten Prognoseverfahrens
Aus den Prognosen berechnen wir das optimal gefüllte Lager als Summe aus den präzise geplanten Bedarfswerten der Ersatzteile zuzüglich Sicherheitsbestand.
Wir wenden hierfür beispielhaft eine in SAP implementierte Formel für den Sicherheitsbestand an:
Sicherheitsbestand = z⋅√(t_LT ) * 1,25 MAD
Hierbei ist
- z ein Sicherheitsfaktor basierend auf dem gewünschten Lieferbereitschaftsgrad,
- t_LT die Wiederbeschaffungszeit (in Tagen),
- MAD die mittlere absolute Abweichung zwischen dem tatsächlichen und prognostizierten (täglichen) Bedarf
Wie hätte es in unserem Beispiel ausgesehen, wenn wir die letzten 30 Tage vorhergesagt hätten? Und darauf basierend unsere Nachbestellungen im Voraus organisiert hätten?
In unserem Fall wählen wir einen Lieferbereitschaftsgrad von 90 %. Mit Hilfe des als bestes identifizierten Prognoseverfahrens erhalten wir sehr genaue Prognosen. Die führen zu einem entsprechend niedrigen Sicherheitsbestand von 0,3. Zu Beginn des Forecast Zeitraums bestellen wir den Sicherheitsbestand. Wir planen, die nächsten 30 Tage genau unsere Prognosen für den jeweiligen Tag nachzubestellen.
Dadurch haben wir die durchschnittliche Lagermenge beträchtlich reduzieren können.
Wichtiger noch:
wir konnten auch Lieferengpässe und Umsatzausfälle für diesen Zeitraum erfolgreich verhindern.
Ist man bereit, höhere Lagerkosten für ein reduziertes Aufkommen von Lieferengpässen in Kauf zu nehmen, kann man den Lieferbereitschaftsgrad in der Formel anheben.
Was kann man noch alles machen, insbesondere bei einer Vielzahl an Ersatzteilen?
Es gibt noch eine Vielzahl weiterer Formeln und Ansätze, um Sicherheitsbestände zu ermitteln, v.a. wenn weitere Parameter, wie z. B. Bestellmengen im Wiederbeschaffungszeitraum oder die Varianz der Wiederbeschaffungszeit, genutzt werden können. Beispielhaft seien hier noch die dynamische Disposition von Gudehus genannt sowie die Möglichkeit, aus zuverlässigen Ober- und Untergrenzen in Form von Prognoseintervallen zu geeigneten Prognose-Konfidenzniveaus Sicherheitsbestände zu bestimmen. Ein Vergleich mehrerer Verfahren analysiert sinnvollerweise die Bestandsentwicklung sowie die erzielbaren alpha- und beta-Lieferbereitschaftsgrade.
Wichtig ist ein dem Unternehmen und Anwendungsfall angepasstes Vorgehen, sowohl in Bezug auf die Verwendung von Prognoseverfahren als auch in Bezug auf die Verwendung von Formeln zur Berechnung des Sicherheitsbestandes. Eine Visualisierung der wichtigsten Analyseergebnisse, z. B. in einem Dashboard, sorgt hier wieder für Transparenz und erleichtert die Analyse und die Entscheidung für ein Vorgehen.
Umsetzung der Maßnahmen zur Bestandsoptimierung bei Ersatzteilen
Letztendlich gilt es, aus den gewonnenen Erkenntnissen dauerhaft Nutzen zu ziehen, indem das beste Vorgehen in die Tat umgesetzt wird.
Relativ einfach ist es, wenn die für am besten befundene Methodik in einem vorhandenen System direkt ausgewählt und die Parameter eingestellt werden können. Im anderen Fall lohnt es sich, eine separate Implementierung in Erwägung zu ziehen, die dem speziellen Fall der Ersatzteile gerecht wird. Gerade in Bezug auf sporadische Zeitreihen ist die Auswahl an passenden Vorhersagemethoden oft begrenzt.
Unsere Empfehlung ist, mit den größten Hebeln zu beginnen und sukzessive weitere Verbesserungen einzuführen und Anpassungen am Vorgehen vorzunehmen. Wer die Ersatzteilplaner und -disponenten einbezieht, hat bessere Chancen, eine Lösung zu erhalten, die genau die Bedürfnisse der Business Experts erfüllt. Auch sind sie entscheidende Player, wenn es darum geht, die neue Lösung als Teil des Planungs- und Dispositionsprozesses zu etablieren. Die Grundvoraussetzung für eine gelungene Lösung ist die Akzeptanz seitens der Business Experts. Mit ihrem Zutun kann die Lösung weiter wachsen und sich verbessern.
Es ist oft eine gute Idee, die neue Lösung zunächst eine Weile parallel zu alten Vorgehensweisen laufen zu lassen und die Unterschiede transparent zu machen. Es erleichtert den Willen, sich auf die neue Lösung zu verlassen, und schult parallel die Nutzer. Wenn die vollständige Akzeptanz da ist und die Prozesse angepasst sind, kann das Augenmerk auf die alten Vorgehensweisen verringert und voll und ganz auf die neue Lösung gelegt werden. Wir haben gezeigt, dass diese dann optimal ist, wenn sie die für den jeweiligen Anwendungsfall beste Vorhersagemethodik mit passenden Sicherheitsbestandsberechnungen kombiniert.
Über prognostica
Wenn Sie Interesse an einer Bestandsoptimierung mittels Prognosemethoden nach State-of-the-Art haben, wenden Sie sich an die prognostica GmbH.
Mit ausgewiesener Expertise in Predictive Analytics, Data Science und künstlicher Intelligenz greift die prognostica GmbH auf eine 10-jährige Beratungserfahrung in Supply Chain und Logistik zurück und hat mit einer Vielzahl an Prognosemethoden — gebündelt in der Forecasting-Software “future” — bereits mehrere Millionen an Bedarfshistorien prognostiziert und so vielen Unternehmen geholfen, ihre Lagerbestände zu optimieren.
Autor Dr. Andre Then

Dr. André Then hat sich während seiner Promotion der mathematischen und datengetriebenen Analyse biochemischer Systeme gewidmet. Seit 2023 verstärkt er als Data Scientist das Team der prognostica unter anderem in den Themen Predictive Analytics und Generative KI.
Autorin Dr. Kristina Krebs

Dr. Kristina Krebs ist Mitgründerin und Business Development Director der prognostica und hat in Mathematik mit dem Schwerpunkt industrielle Statistik promoviert. Sie beschäftigt sich bereits seit 2012 mit datenbasierten Prognosen und ist immer wieder begeistert, wie gut diese gegenüber manuellen Planungen in der Praxis abschneiden.
Download Whitepaper zur Bestandsoptimierung auf Basis mathematisch optimierter Prognosen
Sie können diesen Beitrag zur Prognose-Optimierung für Ersatzteile hier als pdf herunterladen
sofortiger Download
ohne Ihre Daten